算法 - 排序

最经典排序算法：冒泡排序、插入排序、选择排序、希尔排序、归并排序、快速排序、堆排序，计数排序、基数排序、桶排序。

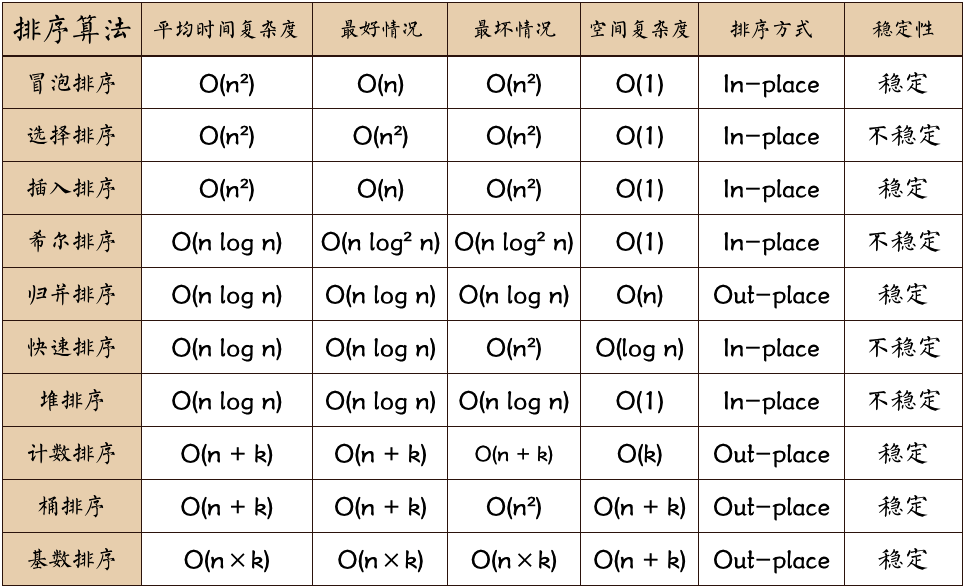
1. 分析排序算法的方法

1. 排序算法的执行效率

   • 最好情况、最坏情况、平均情况时间复杂度

   • 时间复杂度的系数、常数、低阶。排序的可能是 10 个、100 个、1000 个这样规模很小的数据，所以，在对同一阶时间复杂度的排序算法性能对比的时候，就要把系数、常数、低阶也考虑进来。

   • 比较次数和交换（或移动）次数

2. 排序算法的内存消耗

   原地排序（Sorted in place），指空间复杂度为 O(1) 的排序算法。

3. 排序算法的稳定性

   稳定性：指如果待排序序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。如果不变称为稳定排序算法，如果变化则为不稳定的排序算法

   例子：给电商交易系统中的“订单”排序。订单有两个属性，一个是下单时间，另一个是订单金额。如果现在有 10 万条订单数据，希望按照金额从小到大对订单数据排序。对于金额相同的订单，希望按照下单时间从早到晚有序。

   借助稳定排序算法，解决思路是这样的：先按照下单时间给订单排序，注意是按照下单时间，不是金额。排序完成之后，用稳定排序算法，按照订单金额重新排序。两遍排序之后，得到的订单数据就是按照金额从小到大排序，金额相同的订单按照下单时间从早到晚排序的。

2. 冒泡排序（Bubble Sort）

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

2.1 算法实例

要对一组数据 3，5，4，1，2，6，从小到大进行排序。冒泡过程如下：

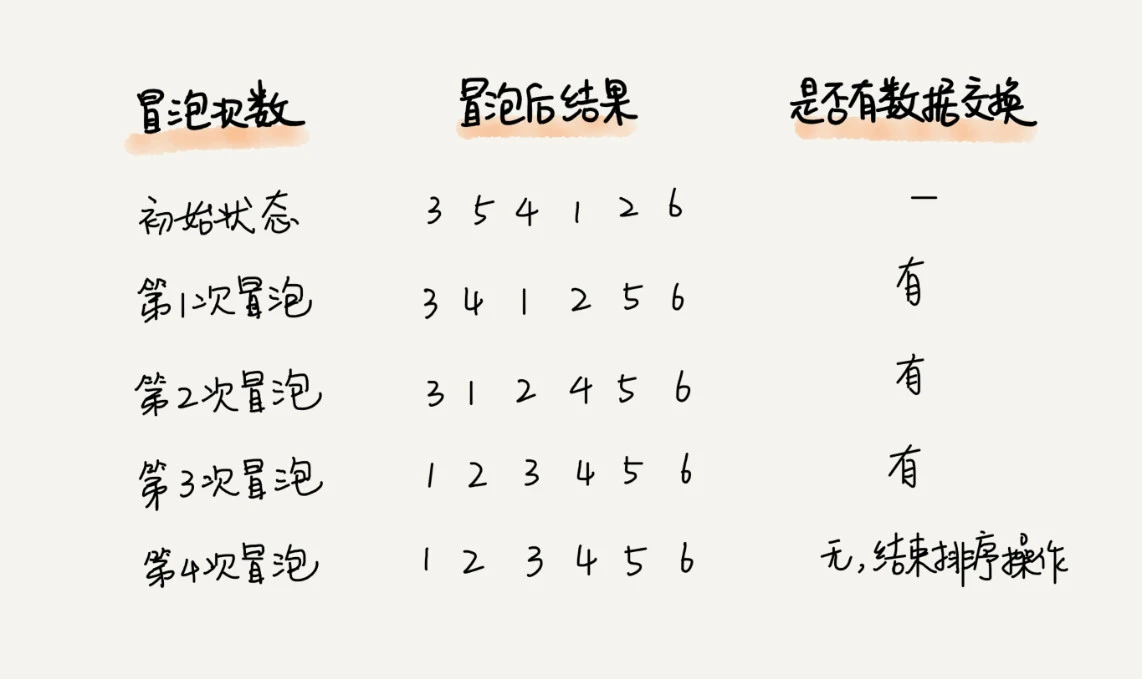
当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。6 个元素排序，正常需要 6 次冒泡操作，而该例子只需要 4 次冒泡操作。

2.2 算法描述

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

2.3 代码实现

// 冒泡排序
public static int[] bubbleSort(int[] array) {
    if (array.length <= 1) {
        return array;
    }

    for(int i = 0; i < array.length; ++i) {
        // 提前退出冒泡循环的标志
        boolean flag = false;
        for (int j = 0; j < array.length - i - 1; ++j) {
        	if (array[j] > array[j+1]) {
                // 交换
                int tmp = array[j];
                array[j] = array[j+1];
                array[j+1] = tmp;
                flag = true; // 表示有数据交换
            }
        }
        if (!flag) {
            break; // 没有数据交换，提前退出
        }
    }
    return array;
}

2.4 算法分析

1. 冒泡算法是否原地排序算法？

   冒泡过程中只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为 O(1) ，是一个原地排序算法。

2. 冒泡排序是否是稳定排序算法？

   在冒泡排序中，只有交换才可以改变两个元素的前后顺序，且相邻的两个元素大小相等是不做交换，顺序不变，所以冒泡算法是稳定的排序算法。

3. 冒泡排序的时间复杂度是多少？

   • 最好情况下，要排序的数据已经是有序了，只需要进行一次冒泡操作，所以最好时间复杂度是 O(n)；

   • 最坏情况下，要排序的数据刚好是倒序排列，需要进行 n 次冒泡操作，所以最坏情况时间复杂度是 $O(n^2)$；

   • 平均情况下，对于包含 n 个元素的数组，这 n 个数据就有 n 的阶乘 $n! = 1*2*...*(n-1)*n$ 种排序方式。元素不同的排列方式，冒泡排序执行的时间肯定不同。通过引入**“有序度”和“逆序度”**来分析：

     有序度：是数组中具有有序关系的元素对的个数，有序元素对：a[i] <= a[j], 如果 i<j

     

     同理对于一个倒序排列的数组，比如 6,5,4,3,2,1，有序度为 0；对于一个完全有序的数组，比如 1,2,3,4,5,6，有序度就是 n*(n-1) / 2，也就是 15，完全有序的数组的有序度叫做满有序度

     逆序度的定义正好跟有序度相反（默认从小到大为有序）：逆序元素对：a[i] > a[j], 如果 i<j

     得到一个公式：逆序度 = 满有序度 - 有序度

     排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了。

     例如：要排序的数组的初始状态是 4，5，6，3，2，1 ，其中，有序元素对有 (4，5) (4，6)(5，6)，所以有序度是 3。n=6，所以排序完成之后终态的满有序度为 n*(n-1)/2=15。

     冒泡排序包含两个操作源自，比较和交换。每交换一次，有序度就加 1。例子中 逆序度 = 15 - 3 = 12，需要进行 12 次交换操作。

     对于包含 n 个数组的数据进行冒泡排序，最坏情况下，初始状态的有序度为 0，所以要进行 $n*(n-1)/2$ 次交换；最好情况不需要进行交换。可以取中间值 $n*(n-1)/4$ 次交换操作，比较操作肯定比交换操作多，且上限是 $O(n^2)$ 所以平均情况下的时间复杂度就是 $O(n^2)$

3. 插入排序（Insertion Sort）

插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

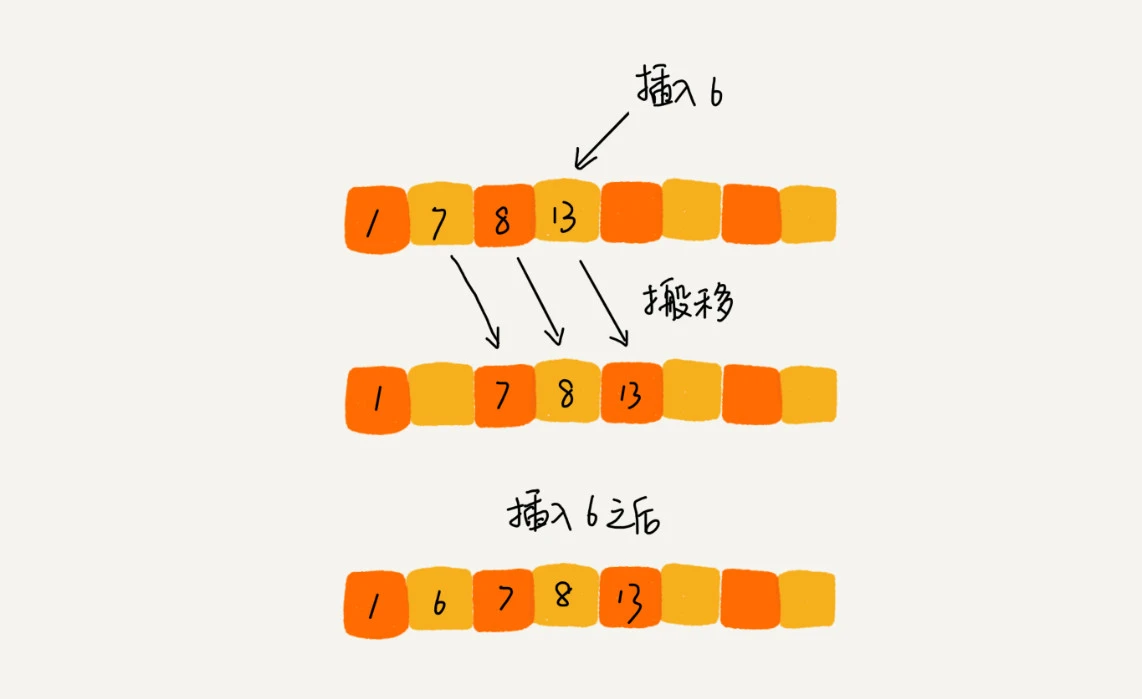
3.1 算法实例

对于一个给定的初始序列，移动操作的次数总是固定的，就等于逆序度。

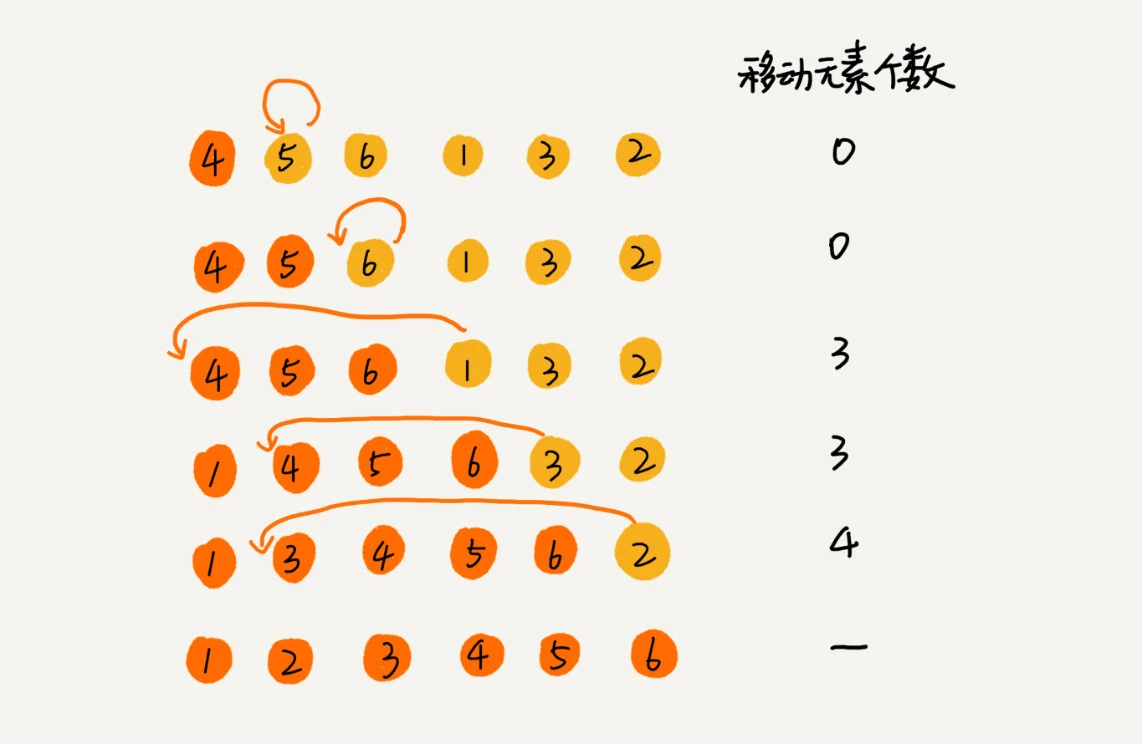
上图例子，满有序度是 n*(n-1)/2=15，初始序列的有序度是 5，所以逆序度是 10。插入排序中数据移动的个数总和也等于 10 = 3 + 3 + 4

3.2 算法描述

插入排序都采用in-place在数组上实现。具体算法描述如下：

• 从第一个元素开始，该元素可以认为已经被排序；
• 取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 如果该元素（已排序）大于新元素，将该元素移到下一位置；
• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 将新元素插入到该位置后；
• 重复步骤2~5。

3.3 代码实现：

// 插入排序
public static int[] insertionSort(int[] array) {
    if (array.length <= 1) {
        return array;
    }

    for (int i = 1; i < array.length; ++i) {
        int curValue = array[i];
        int preIndex = i - 1;
        // 查找插入的位置
        for (; preIndex >= 0; --preIndex) {
            if (array[preIndex] > curValue) {
                // 将前一个元素向后移一个位置
                array[preIndex + 1] = array[preIndex];
            } else {
                break;
            }
        }
        array[preIndex + 1] = curValue;
    }
    return array;
}

3.4 算法分析

1. 插入排序是否是原地排序算法？

   插入排序算法并不需要额外的存储空间，所以空间复杂度为 O(1)，即是原地排序算法。

2. 插入排序是否是稳定排序算法？

   在插入排序中，对于值相同的元素，未改变原来的顺序，所以插入排序是稳定的排序算法。

3. 插入排序算法的时间复杂度是多少？

   • 最好情况下，要排序的数组已经是有序的，无需移动元素，只需循环遍历一遍数组即可，所以最好情况时间复杂度是 O(n)。
   • 最坏情况下，要排序的数组是倒序的，每次后面的元素都需要插入到数组的第一个元素位置，且需要移动大量元素。所以最坏情况时间复杂度是 $O(n^2)$
   • 平均情况下，数组中插入一个元素的平均时间复杂度是 O(n)，所以对插入排序算法来说，需要执行 n 次插入操作，所以平均时间复杂度是 $O(n^2)$

4. 选择排序（Selection Sort）

表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法了吧。

选择排序（Selection-sort）是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

4.1 算法描述

n 个记录的直接选择排序可经过 n-1 趟直接选择排序得到有序结果。具体算法描述如下：

• 初始状态：无序区为R[1..n]，有序区为空；
• 第 i 趟排序 (i=1,2,3…n-1) 开始时，当前有序区和无序区分别为 R[1..i-1] 和 R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录 R 交换，使 R[1..i] 和 R[i+1..n) 分别变为记录个数增加 1 个的新有序区和记录个数减少 1 个的新无序区；
• n-1 趟结束，数组有序化了。

4.2 代码实现

// 选择排序
public static int[] selectionSort(int[] array) {
    if (array.length == 0) {
        return array;
    }
    for (int i = 0; i < array.length; i++) {
        int minIndex = i;
        for (int j = i; j < array.length; j++) {
            // 找到最小的元素
            if (array[minIndex] > array[j]) {
                // 替换最小索引
                minIndex = j;
            }
        }
        // 将索引为 minIndex 和 i 的值互换
        int minValue = array[minIndex];
        array[minIndex] = array[i];
        array[i] = minValue;
    }
    return array;
}

4.3 算法分析

插入排序算法的空间复杂度为 O(1)，即为原地排序算法；相同值时顺序未发生变化，即为稳定的排序算法；最好情况时间复杂度为 O(n)，最坏情况时间复杂度为 $O(n^2)$，平均情况时间复杂度为 $O(n^2)$。

5. 希尔排序（Shell Sort）

6. 归并排序（Merge Sort）

归并排序的核心思想还是蛮简单的。如果要排序一个数组，先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

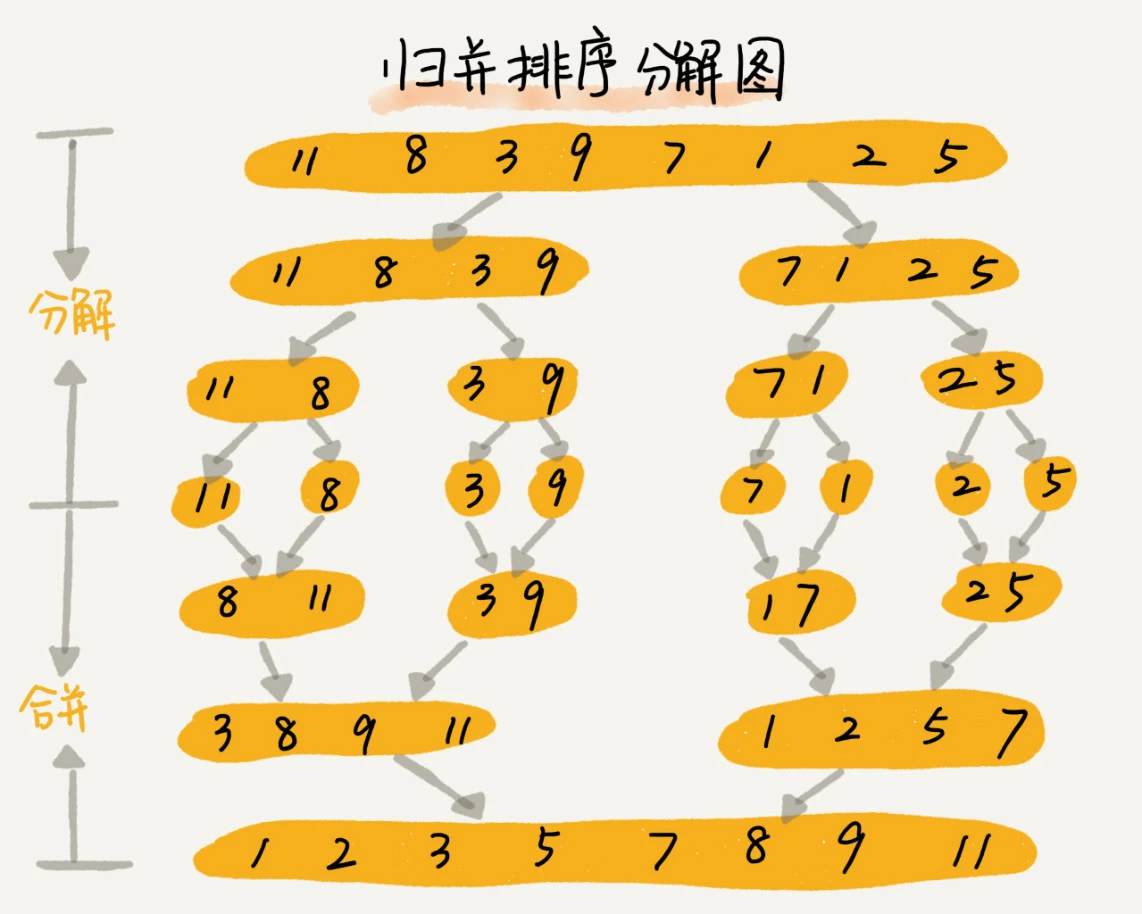
该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。

6.1 算法描述

• 把长度为n的输入序列分成两个长度为 n/2 的子序列；
• 对这两个子序列分别采用归并排序；
• 将两个排序好的子序列合并成一个最终的排序序列。

6.2 代码实现

// 归并排序
public static int[] mergeSort(int[] array) {
    if (array.length < 2) {
        return array;
    }
    int mid = array.length / 2;
    int[] left = Arrays.copyOfRange(array, 0, mid);
    int[] right = Arrays.copyOfRange(array, mid, array.length);
    return merge(mergeSort(left), mergeSort(right));
}

// 归并排序 - 将两个已经排序的数组合并成一个数组并排序
public static int[] merge(int[] left, int[] right) {
    int[] result = new int[left.length + right.length];
    for (int index = 0, i = 0, j = 0; index < result.length; index++) {
        if (j >= right.length) {
            // right 数组都已经放入 result，直接取 left 数组中的元素
            result[index] = left[i++];
        } else if (i >= left.length) {
            // left 数组都已经放入 result，直接取 right 数组中的元素
            result[index] = right[j++];
        } else if (left[i] > right[j]) {
            result[index] = right[j++];
        } else if (left[i] <= right[j]) {
            result[index] = left[i++];
        }
    }
    return result;
}

6.3 算法分析

1. 归并排序是否是稳定排序算法？

   merge 函数中，当相同值的元素合并前后位置没有发生变化，所以归并排序是稳定的排序算法。

2. 归并排序的时间复杂度是多少？

   如果定义求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T( c)，那我们就可以得到这样的递推关系式：T(a) - T(b) + T(c) + K 其中 K等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。

   假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以，套用前面的公式，归并排序的时间复杂度的计算公式就是：

   T(1) = C；   n=1时，只需要常量级的执行时间，所以表示为C。
   T(n) = 2*T(n/2) + n； n>1
   

   进一步分解一下计算过程：

   T(n) = 2*T(n/2) + n
        = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
        = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
        = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
        ......
        = 2^k * T(n/2^k) + k * n
        ......
   

   可以得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，得到 k=log2n 。将 k 值代入上面的公式，得到 T(n)=Cn+nlog2n 。如果用大 O 标记法来表示的话，T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。

   归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

3. 归并排序的空间复杂度是多少？

   归并排序有一个致命的“弱点”，那就是归并排序不是原地排序算法。

   因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。

   递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以归并算法的空间复杂度是 O(n)。

7. 快速排序（Quick Sort）

8. 堆排序 （Heep Sort）

9. 计数排序（Counting Sort）

10. 桶排序 （Bucket Sort）

11. 基数排序（Radix Sort）

来源

• 极客时间《数据结构与算法之美》 (opens new window)专栏笔记
• 十大排序算法：https://mp.weixin.qq.com/s/HQg3BzzQfJXcWyltsgOfCQ